Research
Our interests lie at the interface between theoretical/computational chemistry and biophysics. The current research in the lab is directed towards understanding how biomolecules perform their functions via dynamical motions that are encoded in their three dimensional structures. Ongoing projects include computer simulations of ABC-transporters and development of combined quantum mechanical/molecular mechanical (QM/MM) methods.
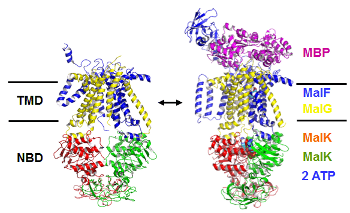
ABC-transporters
Many essential functions of living cells are performed by nanoscale motors consisting of protein complexes. The ability of these biomolecular motors to utilize chemical free energy to perform mechanical work makes them splendid molecular machines. Among various types of molecular motors, ATP-binding cassette (ABC) transporters represent a unique family of motor proteins that enable translocations of various substrates across cell membranes, by harnessing the free energy associated with ATP binding and hydrolysis. Dysfunctions of ABC-transporters have been linked to a number of diseases, including cystic fibrosis, the most common fatal hereditary disease in the US. The over expressions of certain ABC-transporters are also known to contribute to multidrug resistance of tumor cells after cancer patients receive chemotherapy. In bacterial cells, ABC-transporters are responsible for extrusions of various antibiotics. Making using multiscale computer simulations, this project aims at obtaining a deeper understanding of conformational dynamics, enzyme catalysis, as well as the chemomechanical coupling mechanisms under which the chemical free energy is converted into mechanical work in ABC-transporters.
QM/MM development
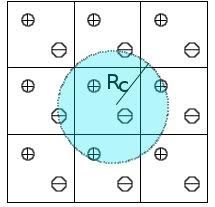
We are developing a methodology to assess long-range interactions in QM/MM simulations. Instead of explicitly calculating the Coulomb potential, we evaluate only pairwise interactions explicitly up to a cutoff distance. Beyond this distance, the long range potential is computed in an average way. This contribution from the virtual images is added to the Fock matrix as a first-order contribution.
Using this approximation we avoid the calculation of the Coulomb contribution in the Fourier space, which in general represents a huge computational effort. The method we use has been named in the literature Isotropic Periodic Sum method and has been applied to numerous systems including biomolecules and ionic systems.[1]
- ↑ Template loop detected: Template:Cite journal